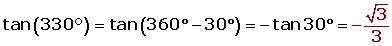Razones trigonométricas
lunes, 31 de octubre de 2011
Ejercicios
Taller
1)Sabiendo que cos α = ¼ , y que 270º <α <360°. Calcular las restantes razones trigonométricas del ángulo α.
Solución:
2)Sabiendo que tg α = 2, y que 180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α.
Solucion:
1)Sabiendo que cos α = ¼ , y que 270º <α <360°. Calcular las restantes razones trigonométricas del ángulo α.
Solución:
2)Sabiendo que tg α = 2, y que 180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α.
Solucion:
3)Sabiendo que sec α = 2, 0< α <  /2, calcular las restantes razones trigonométricas.
/2, calcular las restantes razones trigonométricas.
Solucion:
4)Calcula las razones del siguiente ángulo:
1225°
Solución:
5)Calcula las razones del siguiente ángulo:
330°
Solucion:
6) Comprobar la identidad:
7)Comprobar la identidad:
Solucion:
8)De un triángulo rectángulo ABC, se conocen a = 5 m y B = 41.7°. Resolver el triángulo
solucion:
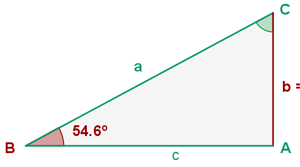
9)De un triángulo rectángulo ABC, se conocen b = 3 m y B = 54.6°. Resolver el triángulo.
Solucion:
10)De un triángulo rectángulo ABC, se conocen a = 6 m y b = 4 m. Resolver el triángulo.
domingo, 30 de octubre de 2011
Webgrafia y Bibliografia
- www.aritutor.com/trigonometria/ejercicios_identidades.html
- w4.icfes.gov.co/AC_EP_Matematicas_2010.pdf
- www.wikipedia.com
- www.clav.sceu.frba.uth_edu.ar
- www.vadenumeros.es
- Trigonometria y geometria analítica, por:C. Hirsht y H.Schoen Editorial:McGRAW-HILL Paginas:43-48 Álgebra y Trigonometria con Geometría Analítica, por:Earl W.Swokowski Editorial:Iberoamericana Paginas:266-286
sábado, 29 de octubre de 2011
Identidades trigonometricas
Las identidades trigonométricas son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos.
Razones trigonometricas
Seno Cosecante
Seno del ángulo B: es la razón entre Cosecante del ángulo B: es la
el cateto opuesto al ángulo y la razón inversa al seno de Bhipotenusa.
Se denota por Sen B Se denota por CosecB
SenB=Cateto opuesto = b CosecB= Hipotenusa = a
Hipotenusa a Cateto opuesto b Coseno Secante
Coseno del ángulo B: es la razón ente Secante del ángulo B: Es la
el cateto adyacente (contiguo) al razón inversa del coseno de Bángulo y la hipotenusa.
Se denota por Cos B Se denota por Sec BCosB=Cateto adyacente = c SecB= Hipotenusa = a
Hipotenusa a Cateto opuesto c Tangente Cotangente
Tangente del ángulo B: Es la razón entre Cotangente del ángulo B: Es la
el cateto opuesto y el cateto adyacente al razón inversa de la tangente
ángulo. de B.
Se denota por TangB Se denota por CtangB
TangB=Cateto opuesto = b CtangB=Cateto adyacente=c
Cateto adyacente c Cateto opuesto b
Problemas de aplicacion
1) Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?
Solucion:
5) Obtener el ángulo que forma un poste de 7.5 m de alto con un cable tirante que va, desde la punta del primero hasta el piso, y que tiene un largo de 13.75 m
6)Obtener la longitud de una escalera recargada en una pared de 4.33 m de altura que forma un ángulo de 60° con respecto al piso.
a) Trazar el triángulo rectángulo anotando los datos e indicando, con una letra, el lado que se desea calcular.
7) Se desea calcular la altura de la torre, para ello se miden los ángulos de elevación desde los puntos A y B. Con los datos de la figura tenemos que:
 SOLUCION:
SOLUCION: 

Solucion:
2) Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 80 m y 130 m, y forman entre ellos un ángulo de 70°.
Solucion:
3)Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30° y si nos acercamos 10 m, bajo un ángulo de 60°.
Solución:
4)Tres pueblos A, B y C están unidos por carreteras. La distancia de A a C es 6 km y la de B a C 9 km. El ángulo que forman estas carreteras es 120°. ¿Cuánto distan A y B?
Solución:
5) Obtener el ángulo que forma un poste de 7.5 m de alto con un cable tirante que va, desde la punta del primero hasta el piso, y que tiene un largo de 13.75 m
Respuesta:
El ángulo formado por el poste y el cable tirante es de 56° 57'
6)Obtener la longitud de una escalera recargada en una pared de 4.33 m de altura que forma un ángulo de 60° con respecto al piso.
a) Trazar el triángulo rectángulo anotando los datos e indicando, con una letra, el lado que se desea calcular.
b) Seleccionar una razón trigonométrica que relacione al ángulo y lado conocidos con el lado que se desea calcular.
e) Obtener el valor natural del ángulo por medio de las tablas trigonométricas o de la calculadora y efectuar las operaciones.
Respuesta:
Por lo tanto, la escalera mide 5 m.
7) Se desea calcular la altura de la torre, para ello se miden los ángulos de elevación desde los puntos A y B. Con los datos de la figura tenemos que:
PROCESO :
Si despejamos h en las dos igualdades e igualamos tenemos:
(10+x)·0'839=1'96·x; 8'39+0'839·x=1'96·x; 8'39=1'121·x; x=7'484 m, aproximadamente.
h=7'484·1'96=14'668. La torre mide unos 14 metros y medio de alto.
8)Se desea construir un puente sobre un río, que mide 10 m de ancho, de manera que quede a una altura de 2 m sobre el agua y que las rampas de acceso tengan una inclinación de 20E. ¿Cuál debe ser la longitud de la baranda?, ¿a qué distancia del cauce se situará el comienzo de la rampa?
9) Si el angulo de elvacion del sol es 42°, ¿cual s la longitud de la sombra proyectada que mide 6.1 pie de altura?
SOLUCION:
Lo hallo con tangente
tan42° = 6.1 pies /longitud
10)Una persona se encuentra en la ventana de su apartamento que está situada a 8m. del suelo y observa el edificio de enfrente. La parte superior con un ángulo de 30 grados y la parte inferior con un ángulo de depresión de 45 grados. Determine la altura del edificio señalado.
SOLUCION:
Primero sacar tangente de 45°
tan= x/ 8m
x= tang 45° x 8m
x= 1 x 8m
x=8m
ese 8 es la distancia horizontal que hay dede la ventana hasta el otro edificio
ahora de nuevo tangente, pero de 60°
tan= 60° x 8m
x= 13.84m
13.84 es la distancia que hay desde el punto horizontal de la ventana hacia la punta del edificio, entonces la altura total del edificio es la suma de:
13,84 + 8m = 21,84m
el edificio 2 mide 21.84m
Suscribirse a:
Comentarios (Atom)